В рамках нашей образовательной программы «Менеджмент игровых проектов» и «Основы создания игр» начинаем выкладывать серию коротких видеороликов по различным нюансам работы геймдизайнера. Сегодня мы поговорим о том, как балансировать головоломки на примере игры в жанре Match-3. Автор видео и материалов геймдизайнер Филипп Кругляков.

Для тех, кому видеоформат неудобен, краткий пересказ. Давайте предположим, что у нас есть массив из 10, 100 или 1000 матч-3 миссий и кривая сложности, которой они миссии должны соответствовать.
Кривая сложности сообщает нам на какой миссии сколько раз должны проигрывать пользователи. Например, если миссия помечена с 90% сложностью, то в среднем лишь 1 из 10 попыток должна быть победной, а если у миссии указана низкая сложность, к примеру, в 20%, то при прохождении миссии игроки должны испытывать в среднем лишь 1 поражение на пять попыток.
Что нам даст соответствие миссий заданной кривой сложности?
Представьте, что у нас есть пачка из 10 миссий. Предположим, что они должны обладать сложностью от 10% до 95%. Исходя из этого мы можем посчитать сколько времени уйдёт у среднего пользователя на то, чтобы пройти эту пачку. Для этого нужно преобразовать % сложности в количество поражений:

Суммировав столбец "кол-во поражений", мы получим 34,7 — это означает, что именно столько раз средний игрок столкнётся с табличкой "Повторить" в процессе прохождения пачки из приведенных 10 миссий.
Если предположить, что за поражение игрок лишается 1 ед. энергии, и 1 ед. энергии восстанавливается 30 минут, то у среднего игрока уйдёт 17 часов на прохождение этих миссий (время, необходимое для восстановления энергии) при условии, что пользователь играет бесперерывно как только накапливает энергию.
Но как же привести миссии в соответствие планируемой сложности? Как не допустить, чтобы в «боевую» версию попали слишком простые или слишком сложные миссии? Как проконтролировать, чтобы миссии соответствовали кривой сложности?
Особенно если речь идёт о матч-3 со сложными механиками, такими как Bing Han Garden.
Один из вариантов балансировки для головоломок доступен каждому даже без применения многоэтажных математических формул. Но придётся пожертвовать временем тестера (или тестеров), который работал бы в связке с левел-дизайнером.
В чём метод работы? А метод заключается в том, что мы не нагружаем левел-дизайнера сложным расчётам, которым он должен действовать. Главное ему осознавать какие механики осложняют работу, какие упрощают, какие геометрические решения миссии насколько затруднят жизнь и т. д. А остальное сделают тестер и аналитика.

Мы видим, что тестер добросовестно отыграл 20 партий и записал сколько он потратил на это ходов (лучше, конечно, чтобы он записывал не вручную, а система автоматически фиксировала), получился массив числел {30, 35, 23, 29, 23, 34 и т. д.}
И это для миссии, чья сложность должна составлять 10% (у игрока должен быть 10% шанс потерпеть поражение)
На основании этих данных (массив попыток от тестера и сложности) мы можем посчитать ограничение по ходам для данной миссии. Если игрок не пройдёт миссию за 34 хода - будем считать, что он проиграл.
Высчитать это можно формулой =ПРОЦЕНТИЛЬ.ВКЛ(массивПопыток; 100% - сложность)
В нашем случае получаем ПРОЦЕНТИЛЬ.ВКЛ({30, 35, 23, 29, 23, 34}; 90%) = 34,1
Функция процентиль может отсутствовать в старых версиях Excel, но даже в этом случае не нужно отчаиваться. Если такой функции нет — её можно написать самому через VBA, но это уже совсем другой урок.
Вот как это выглядит в Excel:

Распространяем формулу на весь столбец и ждём от тестера летспплея:

В качестве заключительного штриха можем задать рамки, что миссия не должна быть слишком длинной или слишком короткой, т. е. "рекомендуемые ходы" не должны находиться вне диапазона, к примеру, от 25 до 34 ходов.

Таким образом левел-дизайнер может увидеть какие миссии слишком долгие - в этом случае он может подкорректировать некоторые решения на миссии, чтобы приблизить достижение цели. И наоборот - какие миссии слишком быстро выполняются и их необходимо усложнить.
Что такое процентиль?
Представьте массив из 6 чисел, к примеру такой {3, 11, 1, 5, 9, 7} , и представьте, что нам нужно выявить для X такое значение, при котором половина чисел массива будет меньше чем X, а другая половина – больше.
Для этого мы должны сортировать массив и получить {1, 3, 5, 7, 9, 11}. Чтобы половина чисел этого массива была больше X – надо взять число по центру из этого массива. В нашем случае по центру располагается два числа 5 и 7, значит берём среднее между двумя этими числами и получим 6.
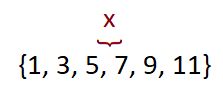
Так вот: в нашем случае число 6 является 50% процентилем для данного массива, так как половина значений превосходит это число.

Если нам нужно подобрать то значение, при котором 75% чисел из перечня будет его превосходить – то мы узнаём 75% процентиль и т. д.
Аналогично могут быть найдены и другие процентили:

Это первая часть цикла по балансу головоломок, продолжение следует. Если вам интересно больше узнать про геймдизайн, создать и запустить свою игру, или пойти на работу в игровую компанию, то приглашаем на наши образовательные программы “Менеджмент игровых проектов” и «Основы создания игр». У нас часто проходят и однодневные открытые мероприятия, узнать о которых можно на странице анонсов.
Автор: Филипп Кругляков
← Назад к списку

